Resistance and Ohms Law
The Ohms Law Triangle Formula
Below are images that explain the formula used in calculating the resistance in relation to the other components of electronics. To use the triangle, cover the value you want to calculate. The remaining letters make up the formula.

Ohm’s Law can only give the correct answer when the correct values are used. Remember the following three rules:
– Current is always expressed in amperes or amps
– Voltage is always expressed in volts
– Resistance is always expressed in ohms
With these rules, the decimal equivalent of figures that are less than 1 should be converted. For example, if the circuit’s voltage is 10 and the current is 200 mA (200 milliamp), the decimal equivalent of the 200 mA, which is 0.20 Amp, should be used in the calculation.
Examples of Solving Ohm’s Law problems
Using the simple circuit below, assume that the voltage supplied by the battery is 10 volts, and the resistance is 5 Ohms.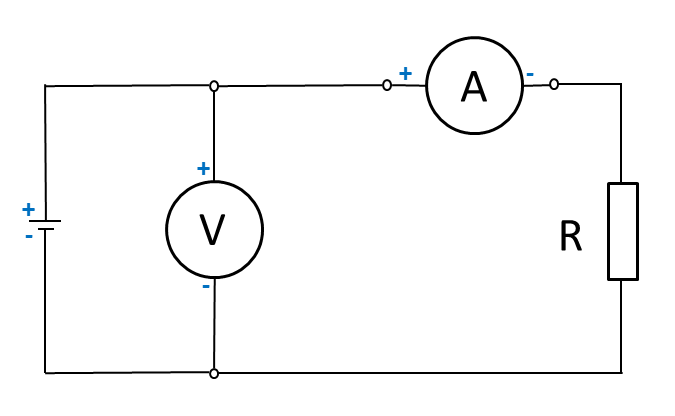
Calculating Current Flow

To find how much current is flowing through the circuit, cover the “I” in the triangle and use the resulting equation.
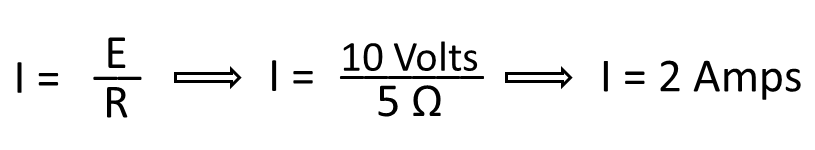
Calculating Circuit Voltage

Using the same circuit, assume the ammeter reads 200 mA and the resistance is known to be 10 Ohms. To solve for voltage, cover the “E” in the triangle and use the resulting equation.
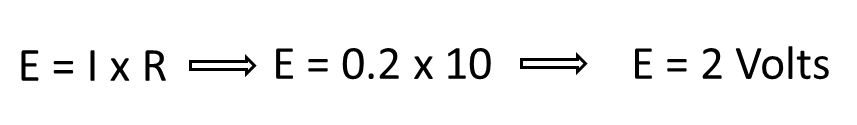
Remember to use the correct decimal equivalent when dealing with numbers that are preceded with milli (m), micro (μ) or kilo (k). In this example 200 had been used, but was converted to 0.2 in the calculation. Otherwise the wrong answer of 2000 volts would have come out as a result.
Calculating Resistance (Ohms)

Using the same circuit, assume the ammeter reads 800 mA and the voltage is known to be 4 Volts. To solve for resistance, cover the “R” in the triangle and use the resulting equation.

Again, remember to use the correct decimal equivalent when dealing with numbers that are preceded with milli (m), micro (μ) or kilo (k). In this example 800 mA has been used, but was converted to 0.8 Ampere in the calculation. Otherwise the wrong answer of .005 Ohms would have come out as a result.
Summary: When we use the triangle to solve the unknown value, the given equivalent figure on the apex of the triangle – in this case is the voltage – is divided by either of the equivalent values at the bottom of the the triangle, whichever is the given meter reading or electronic value. A given value at either side of the bottom of the triangle- the equivalent of the current and resistance – is multiplied by the other bottom value, and vice versa.
